Douglas' Space
차원 축소(Dimensionality Reduction)에 대해 본문
차원 축소(Dimensionality Reduction)에 대해
똘키아빠 2022. 5. 7. 22:01초기에 machine learning의 방법중 unsupervised learning을 설명하면서 차원축소(dimensionality reduction)에 대한 이야기를 한 적이 있습니다. 그리고 얼마전 metric learning, word embedding, transformer 등을 이야기하면서 latent vector, embedding vector 등을 언급한 적이 있습니다. 사실 이 모두가 차원축소의 개념에 포함된다고 이야기할 수 있습니다. 차원축소는 인공지능 분야에서 사용하는 중요한 방법 또는 도구의 하나라고 할 수 있습니다.
차원축소를 단어적으로 쉽게 이해할 수 있는 것은 고차원을 저차원으로 축소한다는 것입니다. 우리가 인지할 수 있는 공간의 개념에서 설명하면, 3차원의 데이타를 2차원의 데이타로, 2차원 데이타를 1차원으로 변환하는 것입니다.

의미적으로 다시 정의한다면 많은 데이타로 부터 이 데이타들의 특징을 표현할 수 있는 적은 양의 데이타로 표현하는 것이라고 할 수 있습니다. 워드임베딩에서 처럼 많은 단어들을 표현하는 고차원의 one-hot vector로 부터 저차원의 embedding vector를 추출하거나, metric learning을 설명할 때 심장병에 대한 많은 데이타속성으로 부터 가장 심장병에 영향을 주는 몇개의 속성만을 선택하는 feature engineering의 예를 들수 있습니다.
조금 더 일반적으로는 고차원의 벡터공간의 데이타로 부터 이 데이타를 가장 잘 설명하는 저차원의 벡터공간으로 매핑하는 것을 차원축소라고 할 수 있습니다. 아래 그림은 고차원의 벡터를 저차원의 벡터로 매핑하는 것을 표현한 것이며, 낮은 차원의 벡터를 latent vector, embedding vector라고 지칭합니다. 이를 또한 다른 말로 encoding한다고 이야기하기도 합니다.

차원축소를 이야기하면 같이 나오는 용어가 차원의 저주(curse of dimensionality)입니다. 차원이 증가할 수록 고차원의 공간에 분포된 학습의 데이타가 부족하여 성능이 저하되는 것을 의미합니다. 다시 말해 차원이 높으면 공간도 늘어나고 이 공간을 채울 수 있는 의미있는 데이타가 되기 위해서는 학습데이타도 그 만큼 많아야 한다는 것입니다. 위의 첫번째 그림에서 알 수 있듯이 축소의 반대의 개념으로 차원이 높아 질수록 공간이 늘어나 빈 공간이 커지게 됩니다.
차원축소를 이해하기 위해 필요한 또 다른 개념이 매니폴드(manifold)입니다. 매니폴드는 고차원의 공간을 저차원으로 매핑하는 subspace를 의미한다고 할 수 있습니다. 고차원의 공간에 분포된 데이타의 특징을 잘 표현하는 subspace인 manifold를 찾는 것이 결국 차원감소의 방법이 되며, 이를 manifold learning이라고도 합니다.
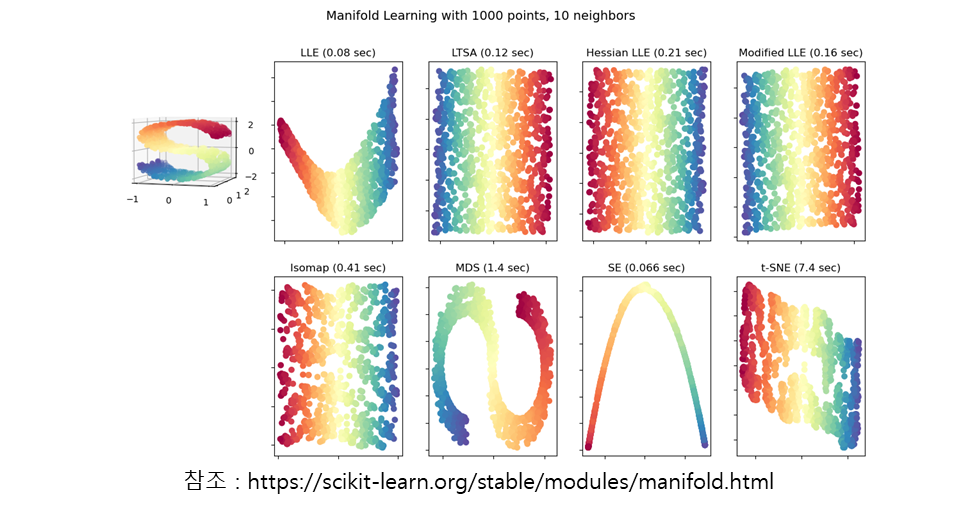
위의 그림은 왼쪽의 3차원의 공간의 swiss-roll 형태의 데이타 분포를 다양한 방법에 의해 표현한 2차원의 manifold들입니다. 차원축소의 대표적인 선형적 방법인 PCA(Principle Component Analysis)의 단점을 해결하는 딥러닝을 이용한 비선형적인 다양한 방법을 보여주고 있습니다.
차원축소는 특징을 잘 추출하여 적은 데이타로 성능을 개선하거나(차원의 저주의 해결, 데이타의 압축, 데이타처리의 효율성 제고 등), 고차원의 벡터공간의 데이타 분포의 특징을 인간이 이해할 수 있는 3차원 이하의 그래픽으로 표현하기 위해 사용합니다.
'Computing Tech. Diary > Artificial Intelligence' 카테고리의 다른 글
| 화자인식기술 (0) | 2022.07.10 |
|---|---|
| 음성인식 및 합성 기술 (0) | 2022.05.29 |
| Federated Learning vs. Distributed Learning (0) | 2022.05.02 |
| Deep Metric Learning (0) | 2022.05.02 |
| DNN의 또 다른 형태, GNN (0) | 2022.05.02 |





